Vibrationsmåling teori

Hvad er vibrationer?

En grundlæggende forståelse:

Der kommer vibrationer fra alle roterende maskiner såsom motore, pumper, generatore og blæsere. Vibrationer kan både høres og mærkes og ved at måle vibrationerne med en sensor, kan man for forudsige en række forskellige maskinfejl som blandt andet: Lejefejl, opretningsfejl, ubalance for blot at nævne nogle få. Hver komponent og fejl har sin egen frekvens og vibration.

For at give en grundlæggende forståelser for vibrationer, hvordan de måles og analyseres, skal vi i det følgende afsnit tale om de to vigtigste termer indenfor vibrationsmåling, nemlig: Waveform og FFT Spektrum, som udgør grundlaget for vibrationsmåling og tolkningen af vibrationer.

Waveform og FFT

Waveform: Forestil dig, at du ryster en vibrationssensor op og ned, præcis lige langt op og ned og med samme kraft, derved fremkommer den øverste graf over tid (et perfekt sinussignal). Eller står og måler ude på en maskine. Det er det rå vibrationssignal, som blot plottes på en graf over tid ud af x-aksen med en bestemt kraft også kaldet amplituden op af Y-aksen. Selve amplituden har tre SI-enheder: Acceleration, Hastighed (Velocity), Forskydning (Displacement).

FFT (Spektrum): En FFT (Forkortelse for Fast Fourier Transform) laves på baggrund af råsignalet fra vibrationssensoren, altså vores Waveform. Forestil dig igen at du står med sensoren og ryster den op og ned med præcis samme kraft, hastighed og afstand, Vi får derved et sinussignal, dette sinussignal har en frekvens alt efter hvor mange gang sensoren rystes op og ned på et sekund. Og naturligvis også en amplitude alt efter hvor voldsomt sensoren rystes.

Med en FFT graf kan man adskille forskellige frekvenser og på den måde se og adskille de forkellige roterende komponenter tydeligt fra hinanden og vurdere deres tilstand.

Amplitude og enheder

Amplitude: Er op af Y-aksen og måles i forskellige enheder, som kan beskrive bevægelsen/vibrationen. For at beskrive en bevægelse op og ned rent fysisk er der tre fysiske karaktere vi skal have på plads:

Acceleration [g]: Acceleration beskriver hvor hurtigt en bevægelse/vibration accelerere og bremses. Acceleration har følgende karaktere:

• Ved lave hastigheder er der lille acceleration.
• Acceleration benyttes ved høje frekvenser.
• Acceleration benyttes ofte ved højhastighedsmaskiner, gearkasser og til lejeanalyse.
• Acceleration er proportionalt med kræfterne indeni maskinen

hastighed [mm/s]: Hastighed beskriver hvor hurtigt en bevægelse/vibration bevæger sig, og er den mest brugte enhed indenfor vibrationsmåling, fordi den har følgende karaktere:

• Hastighed er bedst til at måle frekvenser fra 2-2000 Hz
• Hastighed er proportional med træthed.

Foskydning [mm]: Beskriver hvor langt et ojekt har bevæget sig, altså bevægelsen fra top til bund, hvor langt det er. Særlige karaktere:

• Ved lav frekvens kan forskydningen være høj (Accelerationen lav)
• ved høje frekvenser er forskydningen lav (Accelerationen høj)
• Forskydning er bedst til frekvenser under 10 Hz, eller maskiner under 600 omdrejninger.
• Forskydning er proportional med stress

RMS – simple vibrationsmålinger

Vibrationer kan beskrives som en simpel talværdi og let laves trend over vha. en måling med en overordnet RMS måling (Root Mean Square), som så kan refereres til en alarmgrænse. En sådan værdi beskriver egentlig energiindholdet og kort sagt hvor meget det vibrerer, men ikke hvad der vibrerer eller hvorfor.

Denne værdi giver en overordnet værdi og over tid forventes det at denne trend level stiger, hvis der opstår en begyndende fejl. Dette har dog sine begrænsninger, og man bør ikke stole blot på en enkel talværdi.

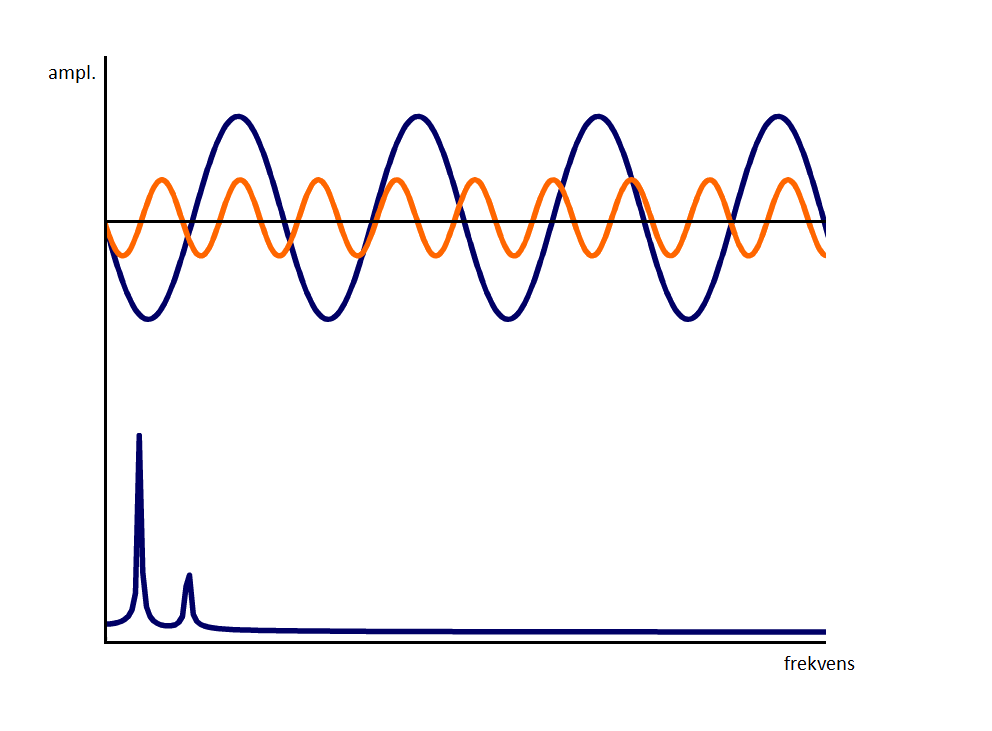
Frekvens

Vi antager at tiden ud af x-aksen er 1 sek. Den øverste graf kaldes tidssignal/Time Waveform og den nederste betegnes som frekvens spektrum/FFT

Hvis vi tager det samme vibrationssignal fra før og tæller “puklerne” på grafen da får vi frekvensen (Hz). Altså hvor mange gange er der sket en hændelse over 1 sekund (Hz), hvor mange gange bevægede sensoren sig op og ned.

Denne frekvens kan aflæses på tidssignalet over tid, men vi kan også afbillede det som vist under sinussignalet med et spektrum (FFT). Hvor vi ændrer akseværdien på x-aksen til frekvens.

Dette skal vise sig at være nyttigt, når flere signaler er blandet sammen, da hver komponent indeni maskinen har hver sin frekvens.

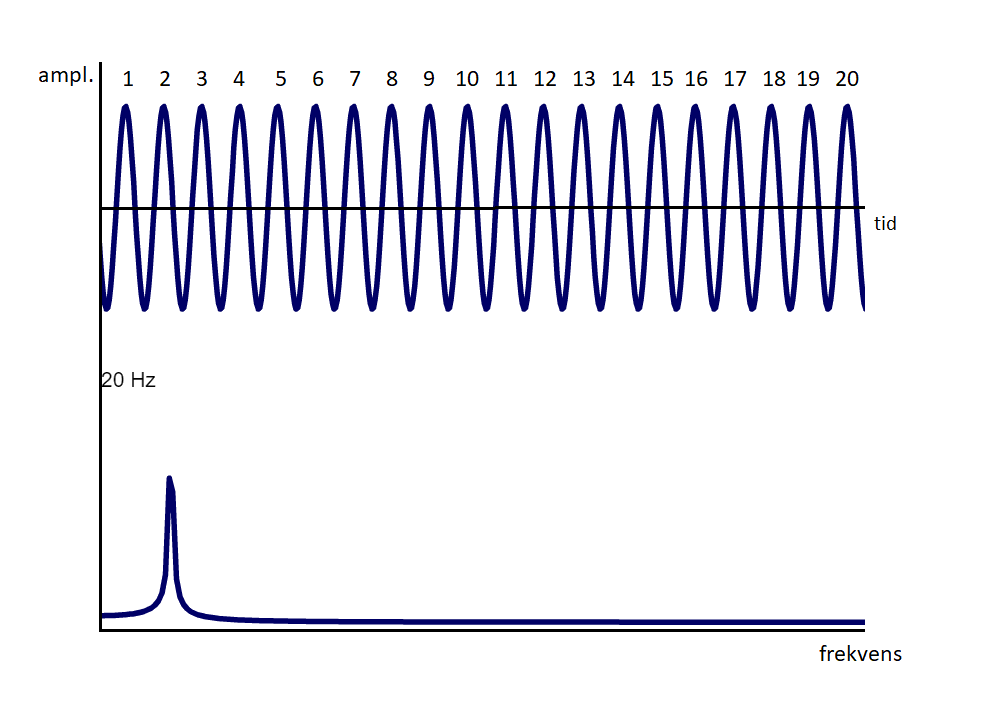
Øget frekvens

Vi antager at tiden ud af x-aksen er 1 sek.

Vi har nu fordoblet frekvensen, derfor er der nu dobbelt så mange “pukler” på vores time waveform. Der er nu 20 pulser på 1 sekund..

Kig nøje på den nederste graf (spektrum – FFT) frekvensen har flyttet sig længere ud af x-aksen, så den nu passer med en frekvens på 20Hz.

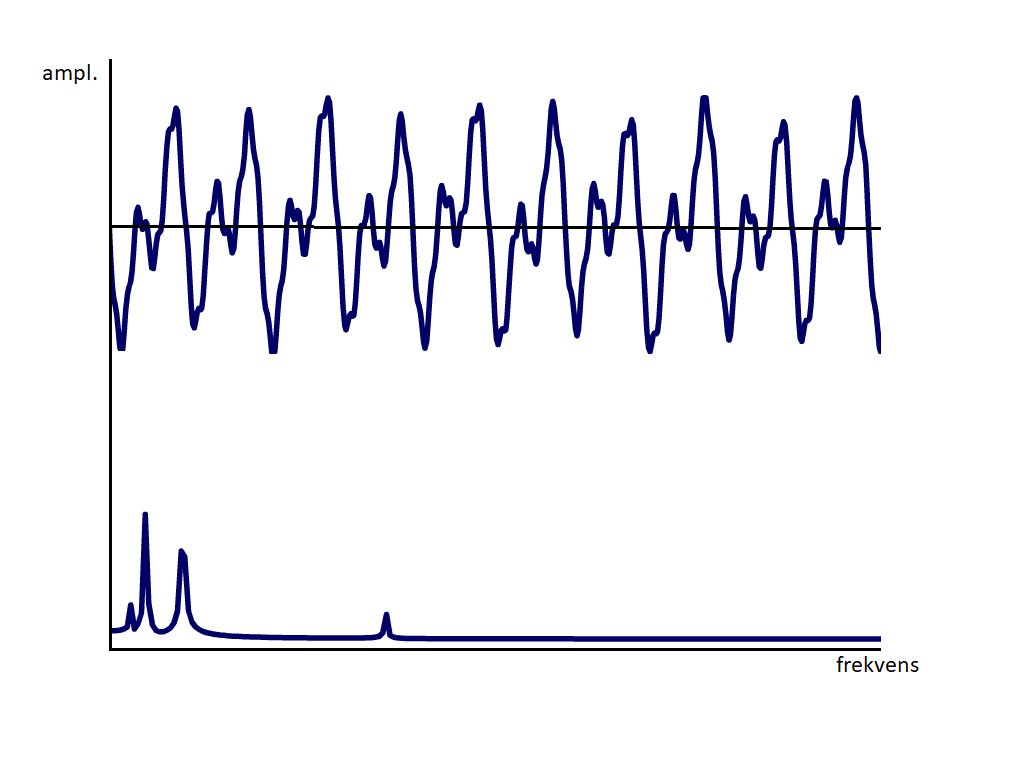
Flere frekvenser

Maskiner har mange forskellige komponenter og rotationshastigheder. Det bliver derfor lidt mere kompliceret, når flere frekvenser blandes sammen som grafen viser.

I maskiner er der komponenter såsom gear, lejer, blæserblade og mange andre komponenter som danner vibrationer. Hver af disse komponenter har deres egen måde at vibrere på, og deres egen frekvens den som vi kan opdele i vores spektrum.

Det skal vise sig straks at blive mere kompliceret, når det er et rigtigt vibrationssignal, og ikke en perfekt sinuskurve som vi har brugt i eksemplerne.